Bias in the LEVIATHAN Stream Cipher

We show two methods of distinguishing the LEVIATHAN stream cipher from a random stream using $2^{36}$ bytes of output and proportional effort; both arise from compression within the cipher. The first models the cipher as two random functions in sequence, and shows that the probability of a collision in 64-bit output blocks is doubled as a result; the second shows artifacts where the same inputs are presented to the key-dependent S-boxes in the final stage of the cipher for two successive outputs. Both distinguishers are demonstrated with experiments on a reduced variant of the cipher.

1 Introduction

LEVIATHAN [5] is a stream cipher proposed by David McGrew and Scott Fluhrer for the NESSIE project [6]. Like most stream ciphers, it maps a key onto a pseudorandom keystream that can be XORed with the plaintext to generate the ciphertext. But it is unusual in that the keystream need not be generated in strict order from byte 0 onwards; arbitrary ranges of the keystream may be generated efficiently without the cost of generating and discarding all prior values. In other words, the keystream is ``seekable''. This property allows data from any part of a large encrypted file to be retrieved efficiently, without decrypting the whole file prior to the desired point; it is also useful for applications such as IPsec [2]. Other stream ciphers with this property include block ciphers in CTR mode [3]. LEVIATHAN draws ideas from the stream ciphers WAKE [9] and SEAL [7], and the GGM pseudo-random function (PRF) construction [1].

The keystream is bounded at $2^{50}$ bytes. Though the security goals are stated in terms of key recovery, it is desirable that distinguishing this keystream from a random binary string should be as computationally expensive as an exhaustive search of the 128 or 256-bit keyspace. Keystream generation is best modelled as a key-dependent function $\textrm{Lev}:\{0,1\}^{48}\mapsto \{0,1\}^{32}$ , mapping a location in the stream to a 32-bit output word; catenating consecutive values of this function from 0 gives the entire keystream:

$\begin{displaymath} \textrm{Lev}(0)\vert\textrm{Lev}(1)\vert\textrm{Lev}(2)\vert\ldots \vert\textrm{Lev}(2^{48}-1)\end{displaymath}$

Finding $\textrm{Lev}(i)$ for arbitrary $i$ is not especially fast. However, once this is done, intermediate values can usually be reused to find $\textrm{Lev}(i+1),\textrm{Lev}(i+2)\ldots$ much more efficiently. This is because the internal structure of the cipher is based on a forest of $2^{32}$ binary trees, each of which generates $2^{16}$ words of output, as shown in Figure 1.

**Figure 1:** Computation of an entire output tree of 8 words with $h=3$ . In the full cipher, $h=16$ and the complete output is built from $2^{32}$ such trees.
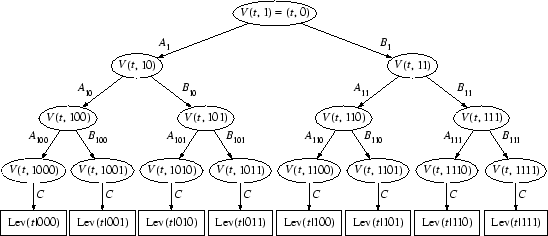
$\resizebox*{1\columnwidth}{!}{\includegraphics{tree.epsi}}$

The notation we use to specify this function precisely is somewhat different from that given in [5], but is convenient for our purposes; we treat $z$ as a parameter, rather than as a word of state. The cipher is parameterised on $n$ and $h$ , where $n$ is divisible by 4 and $n\geq h$ ; LEVIATHAN sets $n=32$ and $h=16$ . $\mid$ denotes catenation of bit strings, $\overline{x}$ bitwise complementation of $x$ , $\oplus$ the XOR operation (addition in $Z_{2}^{n}$ or $Z_{2}^{n/4}$ as appropriate), and $+$ addition in the group $Z_{2^{n}}$ , treating the first bit of the bitstring as the most significant and padding bitstrings shorter than $n$ bits with zeroes on the left. We specify the forest structure illustrated in Figure 1 recursively:

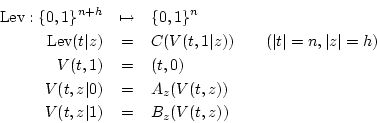
$\begin{eqnarray*} \textrm{Lev}:\{0,1\}^{n+h} & \mapsto & \{0,1\}^{n}\\ \textrm{... ...z\vert) & = & A_{z}(V(t,z))\\ V(t,z\vert 1) & = & B_{z}(V(t,z)) \end{eqnarray*}$

The internal state that functions $A$ , $B$ , and $C$ operate on (and the functions $D$ , $F$ , $G$ used to define them) is a 2-tuple of bitstrings $(x,y)$ ; we treat this as distinct from the catenated bitstring $x\vert y$ . The functions $L$ , $R$ , and $S$ operate on bytes within a word: $L$ and $R$ are rotates, while $S$ provides nonlinearity with the key-dependent permutations $S_{0\ldots 3}$ which map $\{0,1\}^{n/4}$ onto itself. These permutations are generated by the key schedule, which we omit. Note that $F$ and $G$ operate on each word of the tuple independently; mixing is provided by $D$ .

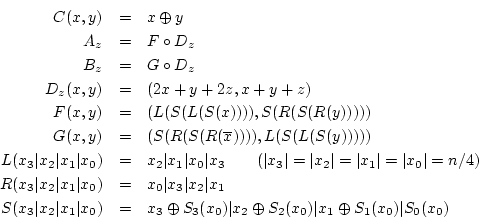
$\begin{eqnarray*} C(x,y) & = & x\oplus y\\ A_{z} & = & F\circ D_{z}\\ B_{z} & ... ...lus S_{2}(x_{0})\vert x_{1}\oplus S_{1}(x_{0})\vert S_{0}(x_{0}) \end{eqnarray*}$

[5] gives a functionally different definition of $D$ ( $D_{z}(x,y)=(2x+y+z,x+y+z)$ ); the one given here is that intended by the authors [4] and used to generate the test vectors, though the difference is not relevant for our analysis.

We present two biases in the LEVIATHAN keystream that distinguish it from a random bit string. We know of no other attacks against LEVIATHAN more efficient than brute force.

2 PRF-PRF Attack

Both attacks focus on consecutive pairs of outputs generated by $\textrm{LevPair}(i)=(\textrm{Lev}(i\vert),\textrm{Lev}(i\vert 1))$ . Clearly, LevPair generates the same $2^{50}$ -byte keystream as Lev, so a distinguisher for one is a distinguisher for the other. Such pairs are interesting because they are the most closely related outputs in the tree structure; [5] refers to attacks using such pairs as ``up-and-down attacks''. We can expand the formula for LevPair as follows:

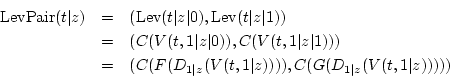
$\begin{eqnarray*} \textrm{LevPair}(t\vert z) & = & (\textrm{Lev}(t\vert z\vert),... ...D_{1\vert z}(V(t,1\vert z)))),C(G(D_{1\vert z}(V(t,1\vert z))))) \end{eqnarray*}$

From this we define functions LevAbove which generates the last common ancestor of such an output pair as illustrated in Figure 2, and PairCom which generates the output pair from the ancestor:

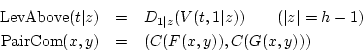
$\begin{eqnarray*} \textrm{LevAbove}(t\vert z) & = & D_{1\vert z}(V(t,1\vert z))\... ...z\vert=h-1)\\ \textrm{PairCom}(x,y) & = & (C(F(x,y)),C(G(x,y))) \end{eqnarray*}$

**Figure 2:** Final stage of LevPair output; LevAbove finds the last common ancestor of the pair.
$\resizebox*{!}{4.8cm}{\includegraphics{abc.epsi}}$

This structure gives us our first distinguisher. Though PairCom has the same domain as range, it is not in general bijective; it can be modelled more accurately as a random function. Thus a collision can occur in LevPair, given two distinct inputs, if there is a collision either in LevAbove or in PairCom, and if we model both as random functions the probability of an output collision for two random distinct inputs to LevPair is thus approximately $2^{-2n}+(1-2^{-2n})2^{-2n}\approx 2^{1-2n}$ , twice what it should be if the keystream were a random binary string.

For $n=32$ , this increased probability of collisions between output word pairs can be observed with a birthday attack after around $2^{33}$ output pairs ( $2^{36}$ bytes) have been generated; the techniques of [8] may be used to reduce the memory demands of this attack, though this slows the attack by a factor of approximately $(h+1)/4=4.25$ where $h$ is the height of the tree, since probes can no longer take advantage of the higher efficiency of sampling consecutive values of LevPair.

3 S-Box Matching Attack

The definitions of the $F$ and $G$ functions are very similar; $G$ is the same as $F$ except that it treats its inputs in the opposite order, and inverts one of them. If $G$ did not apply bitwise inversion to its first input (call this function $G'$ ), then the two functions would be related by $F\circ \textrm{Swap}=\textrm{Swap}\circ G'$ (with Swap having the obvious definition $\textrm{Swap}(x,y)=(y,x)$ ); this would mean in turn that $F(a,a)=\textrm{Swap}(G'(a,a))$ for any $a$ , and thus that $C(F(a,a))=C(G'(a,a))$ , with the result, as we shall see, that repeating pairs were visible in the output roughly twice as often as they should be. The inversion on the first input of $G$ breaks this symmetry; however, it turns out that it does not prevent a related attack.

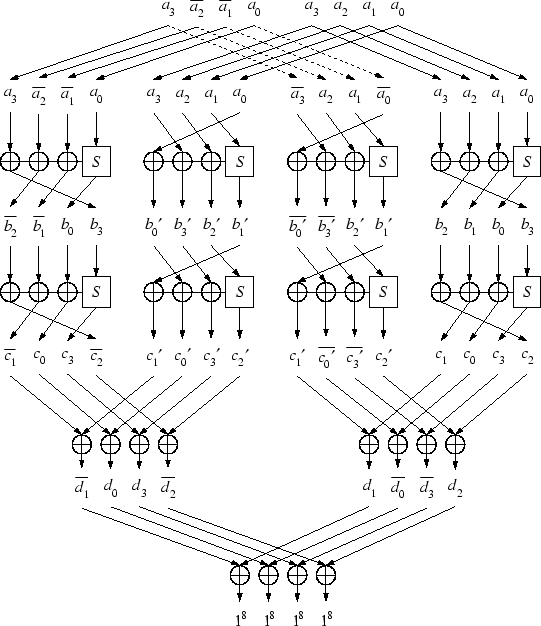
Computation of PairCom requires 32 S-box lookups, but for each computation of the $S$ function the same 8-bit index, drawn from the least significant byte, is fed to each of the four S-boxes. Changes to the other bytes carry directly into the output of $S$ , without nonlinearity or mixing; in other words, where $\Delta x=\Delta x_{3}\vert\Delta x_{2}\vert\Delta x_{1}\vert^{n/4}$ , we find $S(x\oplus \Delta x)=S(x)\oplus \Delta x$ . We call this least significant byte the index to the S-box. If $(x,y)$ is the input to PairCom, only bytes $x_{3},x_{0}$ of $x$ are indices to S-boxes in $F$ , and only bytes $x_{2},x_{1}$ are indices in $G$ ; by inverting only these two bytes in our pair $(a,a)$ , we can avoid the symmetry-breaking effect of the inversion as far as the nonlinear components are concerned, which results in the same four S-box indices being used in both the $F$ and $G$ branches of PairCom.

**Figure 3:** S-box matching input to $C\circ \textrm {PairCom}$ . The function $F$ is on the left, $G$ on the right, and $C$ underneath; dotted lines indicate bitwise inversion (the first step of the $G$ function) and the `` $\oplus \oplus \oplus S$ '' symbol represents the function $S(x_{3}\vert x_{2}\vert x_{1}\vert x_{0})=x_{3}\oplus S_{3}(x_{0})\vert x_{2}\oplus S_{2}(x_{0})\vert x_{1}\oplus S_{1}(x_{0})\vert S_{0}(x_{0})$ .
$\resizebox*{1\textwidth}{!}{\includegraphics{stefan.epsi}}$

Figure 3 illustrates this attack. For an arbitrary $n$ -bit string $a=a_{3}\vert a_{2}\vert a_{1}\vert a_{0}$ , we define symbols for intermediate values in $F(a,a)$ :

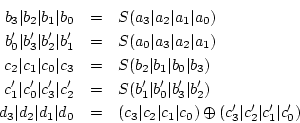
$\begin{eqnarray*} b_{3}\vert b_{2}\vert b_{1}\vert b_{0} & = & S(a_{3}\vert a_{2... ...}\vert c_{0})\oplus (c'_{3}\vert c'_{2}\vert c'_{1}\vert c'_{0}) \end{eqnarray*}$

With these definitions, we find that $\textrm{PairCom}(a_{3}\vert\overline{a_{2}}\vert\overline{a_{1}}\vert a_{0},\... ...verline{d_{2}},\: d_{1}\vert\overline{d_{0}}\vert\overline{d_{3}}\vert d_{2})$ :

$\begin{eqnarray*} C(F(x,y)) & = & C(L(S(L(S(x)))),\; S(R(S(R(y)))))\\ & = & C(... ...& = & d_{1}\vert\overline{d_{0}}\vert\overline{d_{3}}\vert d_{2} \end{eqnarray*}$

From this it is clear that for any input of the appropriate form, one output word is the inverse of the other; or in other words, if we now XOR the two word outputs from PairCom together (which, conveniently, is the same as applying the LEVIATHAN compression function $C$ a second time), we find

$\begin{eqnarray*} C(\textrm{PairCom}(a_{3}\vert\overline{a_{2}}\vert\overline{a_... ...d_{1}\vert\overline{d_{0}}\vert\overline{d_{3}}\vert d_{2}=1^{n} \end{eqnarray*}$

Since we model LevAbove as a random function we conclude that inputs to PairCom have probability $2^{-n}$ of matching this form in the normal calculation of LevPair. Where inputs do not match this form, we assume that PairCom behaves as a random function and therefore that for random $(x,y)$ not matching this form, $\textrm{Pr}\left( C(\textrm{PairCom}(x,y))=1^{n}\right) =2^{-n}$ ; this assumption is borne out by experiment. From this we conclude that LevPair is twice as likely as a random function to produce an output $(x_{0},x_{1})$ such that $C(x_{0},x_{1})=1^{n}$

$\begin{displaymath} \textrm{Pr}\left( C(\textrm{LevPair}(t\vert z))=1^{n}\right) =2^{-n}+(1-2^{-n})2^{-n}\approx 2^{1-n}\end{displaymath}$

For $n=32$ , a test for the presence of this bias should therefore take on the order of $2^{33}$ samples of LevPair, ie $2^{36}$ bytes, as for the previous attack.

4 Experiments

For the PRF-PRF attack, we ran over 256 distinct keys generating $N=6291456$ 32-bit LevPair outputs for each, and sorting them to find collisions. We count as a collision each instance where a distinct pair of inputs result in the same output; thus, where $m>2$ outputs have the same value, we count this as $m(m-1)/2$ distinct collisions. For a random function we would expect to find approximately³ $256(N(N-1)/2)/2^{2n}\approx 1179678$ collisions in total across all keys, while the PRF-PRF attack would predict an expected $256(N(N-1)/2)/2^{2n-1}\approx 2359296$ . The experiment found 2350336 collisions; this is $1077.9$ standard deviations (SDs) from the expected value in the random function model, and $5.83$ SDs from the expected value in the model provided by the PRF-PRF attack. This shows that this model identifies a substantial bias in the cipher, but there is a further bias in the collision probability of roughly 0.38% yet to be accounted for.

For the S-box matching attack, we generated $N=16777216$ LevPair outputs for each of 256 keys, counting outputs with the $C(x,y)=1^{32}$ property. A random function would generate an expected $256N/2^{16}=65536$ such outputs, while the S-box matching attack predicts that LevPair will generate an expected $256N/2^{15}=131072$ such outputs. The experiment found $135872$ such outputs; this is $274.8$ SDs from the expected value in the random function model, and $13.26$ SDs from the expected value in the model provided by the S-box matching attack. Again, this shows that while a substantial source of bias has been identified, there is still a bias of 3.66% yet to be accounted for. Scott Fluhrer has reported finding this attack effective in experiments against the full LEVIATHAN with $n=32,h=16$ .

5 Conclusions

We have shown two forms of bias in the output of the LEVIATHAN keystream generator, either of which distinguish it from a random function with $2^{36}$ known bytes of output; we have not as yet found a way to recover key material using these distinguishers. These distinguishers can both be applied to the same portion of keystream for greater statistical significance. Both make use of compression in the PairCom function.

Despite these attacks, LEVIATHAN demonstrates that a tree-based cipher could offer many advantages. It is to be hoped that similar designs, offering the same speed and flexibility but resistant to this and other attacks, will be forthcoming.

Acknowledgements

Thanks to Rüdiger Weis for helpful commentary and suggestions, and to the LEVIATHAN authors for providing an implementation of the first experiment and for useful discussion.